University of Silesia in Katowice

|tekst: Michalina Piątek, student of the Mathematics degree programme|
|Anna Glenszczyk, PhD, tutor|
|This article was written for the Logic Workshop|

Where do the numbers come from? A short story on the numbers history

A number does not have a definition, to be honest…

‘Number’ seems to be an abstract term. Defining it is problematic, because there is no sensible answer to the question: What is a number? The word itself gives us no information on the abstract object we are considering. However, we can ‘indicate’ numbers in our everyday life.
The number of cross buns purchased in Biedronka (or Lidl, if you prefer) can be characterised by a specific natural number; the number of points scored on the test, final exam, by a rational number (perhaps even an irrational number, if someone tried hard). However, please note that none of these numbers is not a number per se. Each of them is definite – either natural, or rational, or irrational. So it is clear that the number must be somehow specific. This would make sense, because by trying to define a number as an element belonging to the set of all numbers, we would arrive in a twisted way (probably in a metric-river) at Russell’s antinomy.
From now on, I will try (to the best of my, as Paul Erdős would probably call it, epsilon capabilities) to describe numbers professionally, that is, as objects that satisfy established axioms and operations.

Which numbers were first?

Of course, I ask which numbers appeared as first. Prime numbers probable were not among those discovered at the beginning. Naturally (pun not intended), we can assume that the basic numbers we deal with are natural numbers. After all, they have always been with us. Prehistoric people incised bones, such as the Ishago bone, and these incisions were meant to symbolise something. Unfortunately, we don’t know what, but certainly something countable. What’s interesting, in the case of bone from Ishago coincides with prime numbers between 10 and 20.

Someone may ask ‘ok, but where did these numbers come from?’. A trivial and not so funny answer would be ‘a stork brought them’. However, if we take the number 0 (or the empty set) as a stork, then in the universal, axiomatic construction of natural numbers proposed by Giuseppe Pean These conditions must be met by any construction of natural numbers.

Starting from 0 and defining the successor of a natural number, we are able to construct a set of natural numbers. For the number 0 “naturalness by definition” is enough (providing that we assume by definition that 0 is a natural number). Successor (often denoted S(a)) needs a bit more conditions. The most important are:

1. Every natural number a has its successor, S(a)
2. 0 can’t be the successor of any natural number
3. if the successors of two natural numbers are the same, i.e. S(a)=S(b) then these numbers are equal to each other a=b

Then I should mention the model of von Neumann. In this case, we identify finite sets with natural numbers. 0 will correspond to Ø. How is the consequent of S(a) defined? As a sum of the set a with the singleton {a} (i.e. a single-element set containing only a):

S(a) = a 𝖴 {a}. It’s not hard to notice that now:

0 = Ø, 1 = {Ø}, 2 = {Ø, {Ø}}, 3 = {Ø, {Ø}, {Ø, {Ø}}} i tak dalej.

This model also shows mathematical induction in a beautiful way.

(Un)natural numbers

Great. One set of numbers done. We already know where they come from – very wise men, Peano and von Neumann figured it out. And what next? Going back to Ancient Greece, we can find rational numbers constructed as ratios of the lengths of the sides. A little later, an exact definition of the rational numbers was invented. The fractions p/q and r/s correspond to the equivalence relation ~ defined as:

(𝑝, 𝑟) ~ (𝑞, 𝑠) ↔ 𝑝 ∙𝑠=𝑟 ∙𝑞

Just the question is: what are p, r, q and s? Knowing the terms from algebra, we will call them ‘elements of the field’. However, we are at the Logic Classes and we are using the definition of relations, so it is logical that the pairs (p, r) and (q, s) are the elements of the Cartesian quotient of two sets. The question arises: which ones?

We can’t forget about integers, which are also “derived” from natural numbers. We can also algebraically define integers as being the opposites of natural numbers. However, if we extrapolate Pean’s axioms in the other direction and define antecedents in addition to the consequents, we obtain a set of integers.

Avoiding the ‘what came first, integers or rationals?’ war, let’s assume that the elements p, r, q, s belong to the integers. With the assumption that r and q are different from 0, of course. Since kindergarten we’ve been taught that we can’t divide by 0. The relation ~ is then described by the Cartesian product of two Cartesian products of sets of integers, the secondary without 0.

~ ⊂ (ℤ× ℤ\{0})×(ℤ× ℤ\{0})

And what’s next?

After all, we already know that numbers don’t end with rational numbers (positive or negative). We still have to characterise algebraic, real, transcendental and complex numbers. In total, maybe let the positive real numbers be all possible lengths. And let the negative reals be their opposites. And an imaginary unit: well, let’s draw a complex plane and we even have a pretty well visible set of all complex numbers. Every point on this plane corresponds to some complex number, specifically one. And that’s all, I guess. Or not? Is it the end of the essay?

No. Wait a second. After all, there are also some strange Hebrew numbers. Something like… Alef zero? This funny N… Okey, I got this, I copied it from the signboard – ℵ₀. Okay, but where do we place it? Oh, okay, those are the so-called cardinal numbers. So it’s agreed, they’re numbers, but where can we put them on this complex plane? Well, unfortunately we can’t. But they’re still numbers. They are applicable. They can also be constructed and describe specific mathematical objects, sets. It is worth mentioning that in this case we are already considering whole classes of numbers. This makes sense because we’re starting to talk about sets of numbers based on larger and larger sets. And Russell’s antinomy and its consequences need no introduction (this is an obvious topic for anyone who has come across the concept of the power of sets; I would explain it in amazingly simple terms, unfortunately the margin is too small to contain it).

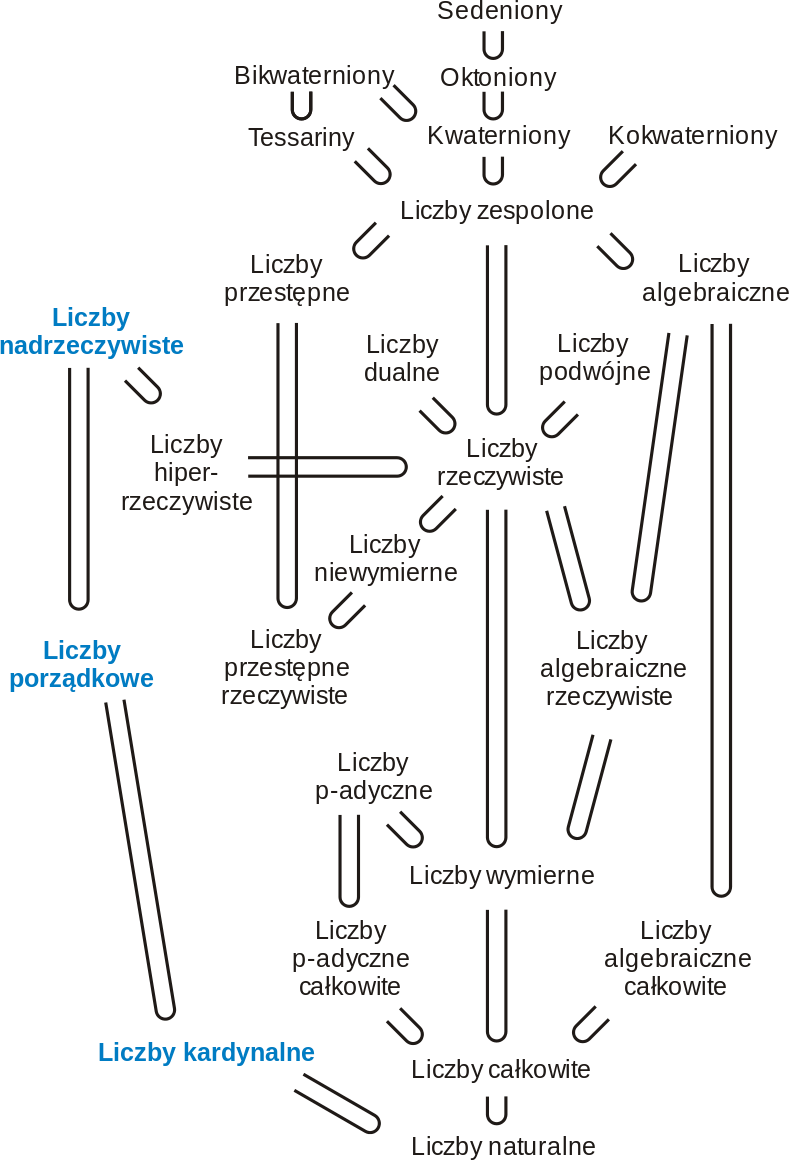
As it turns out, there are much more of them! On Wikipedia (which has been – within limits – my inspiration) there is even a very nice .png file showing these “most important” number sets. Or rather, the most frequently considered ones. There are ordinal numbers above the cardinal numbers. And a category above them, in their superclass we can find hyperreal numbers. But going in a different direction, but also from natural numbers, we arrive at real numbers, complex numbers, quaternions, and other hypercomplex numbers.

Topic: “Where do the numbers come from?”. After of all, the time has come to answer this extremely difficult question. The question, and the answer to it, on which depends the sense of writing this column for the last 65 minutes.

Rys. 1: Hasse diagram showing sets and number classes, and the inclusion relations between them.
SourceŹródło: https://pl.wikipedia.org/wiki/Liczba

Where do the numbers come from?

After an in-depth few hours of research and a few more hours of writing, we came to fundamental conclusions. To paraphrase Voltaire, it can be said that:

If there were no numbers in the world, it would be necessary to invent them.

But which numbers? The one we need at the moment. If the construction turns out to be correct and there is no contradiction in the axioms, then there is nothing to prevent this newly created/discovered (whether it was created or discovered is a topic for the next essay) set or class from determine them with the use of numbers.

But what can we say about the numbers we already “have”? Where did they come from? Let us note that all numbers in a sense come from the set of natural numbers, they are its extension or exclusion from some set (also composed of natural numbers). Similarly, transcendental numbers are actually real numbers (constructed from natural numbers) that are not algebraic numbers (which were also constructed from natural numbers).

Let’s say all other numbers came from natural numbers.

But where did the natural numbers come from? Their construction actually started with 0 (or Ø). Zero, empty set, nothing. Concluding the essay poetically, it turns out that, paradoxically… the numbers came from nothing.

Thank you for your attention and reading the story about the numbers history😊