„Skąd się biorą liczby?”
Oto przedstawiamy krótką historię historii liczb…
NAUKA | MOJA PASJA
Nauka – według definicji ze Słownika Języka Polskiego to ogół wiedzy ludzkiej ułożonej w system zagadnień, ale także zespół poglądów stanowiących usystematyzowaną całość i wchodzących w skład określonej dyscypliny badawczej.
Nauka to także czynność: uczenie się czegoś lub uczenie kogoś.
Zapraszamy do lektury cyklu Nauka | Moja Pasja, w którym nasi młodzi badacze prezentują, nad czym pracują oraz pokazują, że nauka i proces badawczy mogą wciągnąć na dobre.
|tekst: Marcin Aleksa, student kierunku matematyka|
|dr Anna Glenszczyk, opiekun|
|Praca została napisana na potrzeby Warsztatów z logiki|
Skąd się biorą liczby? – krótka historia o historii liczb
Liczba nie ma definicji szczerze…
Liczby wydają się pojęciem stricte abstrakcyjnym. Samo ich zdefiniowanie stanowi problem, nie istnieje bowiem sensowna odpowiedź na pytanie: Czym jest liczba? Samo słowo w sobie nie daje nam żadnej informacji o tym abstrakcyjnym obiekcie, który rozpatrujemy. Jednak potrafimy „wskazać” liczby w codziennym życiu.
Liczbę zakupionych bułek w Biedronce (lub Lidlu, jak kto woli) możemy scharakteryzować przez konkretną liczbę naturalną, liczbę zdobytych punktów na teście, maturze, egzaminie przez liczbę wymierną (być może nawet niewymierną, jeśli ktoś bardzo się postarał). Zauważmy, że jednak żadna z tych liczb nie jest liczbą per se. Każda z nich jest określona – albo naturalna, albo wymierna, albo niewymierna. Tak więc jasno widać, że liczba musi być jakaś. Co miałoby sens, bo próbując zdefiniować liczbę jako element należący do zbioru wszystkich liczb doszlibyśmy pokraczną drogą (prawdopodobnie w metryce-rzece) do antynomii Russella.
Od teraz postaram się (w miarę moich, jakby to Paul Erdős zapewne nazwał, epsilonowych możliwości) opisywać liczby fachowo, to znaczy jako obiekty spełniające ustalone aksjomaty i działania.
Które liczby były pierwsze?
W pytaniu chodzi oczywiście o te, które pojawiły się najwcześniej. Liczby pierwsze raczej nie były pierwszymi, jakie ludzkość odkryła. Naturalnie (gra słowna niecelowa) możemy założyć, że podstawowymi liczbami, którymi się zajmujemy będą liczby naturalne. W końcu towarzyszą nam od zawsze. Prehistoryczni ludzie nacinali kości, takie jak kość z Ishago, których nacięcia miały coś symbolizować. Niestety nie wiemy co, ale z pewnością coś policzalnego. Co ciekawe, w przypadku kości z Ishago nacięcia pokrywają z liczbami pierwszymi pomiędzy 10 i 20.
Ktoś powie „No dobra, ale skąd się te liczby naturalne wzięły?”. Trywialną i mało śmieszną odpowiedzią byłoby „bocian je przyniósł”. Jeśli jednak przyjmiemy za bociana liczbę 0 (lub zbiór pusty) to uniwersalnej, aksjomatycznej konstrukcji liczb naturalnych dostarcza definicja zaproponowana przez Giuseppe’a Peana. Warunki te muszą być spełniony przez każdą konstrukcję liczb naturalnych.
Zaczynając od 0 i definiując następnik liczby naturalnej jesteśmy w stanie skonstruować zbiór liczb naturalnych. Liczbie 0 wystarczy „naturalność z definicji” (tzn. przyjmujemy z definicji, że 0 jest liczbą naturalną). Następnik (często oznaczany jako S(a)) potrzebuje nieco więcej warunków. Najważniejsze z nich to:
- dla każdej liczby naturalnej a istnieje jej następnik, S(a)
- 0 nie jest następnikiem żadnej liczby naturalnej
- jeśli następniki dwóch liczb naturalnych są takie same, tzn. S(a) = S(b) to te liczby są sobie równe a = b
Warty przytoczenia jest model von Neumanna. W tym przypadku z liczbami naturalnymi utożsamiamy zbiory skończone. 0 będzie odpowiadało Ø. Jak definiowany jest następnik S(a)? Jako suma zbioru a z singletonem {a} (czyli zbiorem jednoelementowym, zawierającym jedynie a):
S(a) = a 𝖴 {a}. Nie jest ciężko zauważyć, że teraz:
0 = Ø, 1 = {Ø}, 2 = {Ø, {Ø}}, 3 = {Ø, {Ø}, {Ø, {Ø}}} i tak dalej.
Model ten również w piękny sposób pokazuje wprost indukcję matematyczną.
Liczby nienaturalne
No i super. Jeden zbiór liczb z głowy. Wiemy już skąd się biorą, bardzo mądrzy panowie Peano i von Neumann znaleźli na to sposób. A co po liczbach naturalnych? Wracając do czasów Starożytnej Grecji możemy znaleźć liczby wymierne, skonstruowane jako stosunki długości boków. Nieco później wymyślono dokładną definicję liczb wymiernych. Ułamkom p/q oraz r/s odpowiada relacja równoważności ~ określona jako:
(𝑝, 𝑟) ~ (𝑞, 𝑠) ↔ 𝑝 ∙ 𝑠 = 𝑟 ∙ 𝑞
Tylko pytanie czym są p, r, q i s? Znając określenia z algebry nazwiemy je elementami ciała. Jesteśmy jednak na Warsztatach z logiki i korzystamy z definicji relacji, więc logiczne jest, że pary (p, r) i (q, s) są elementami ilorazu kartezjańskiego dwóch zbiorów. Pytanie narasta jakich?
Nie możemy zapomnieć o liczbach całkowitych, które również „wywodzą się” od liczb naturalnych. Liczby całkowite jesteśmy w stanie również algebraicznie zdefiniować poprzez bycie elementami przeciwnymi do liczb naturalnych. Jednakże ekstrapolując aksjomatykę Peana w drugą stronę i definiując oprócz następników poprzedniki uzyskamy zbiór liczb całkowitych.
Unikając wojny „co było pierwsze, liczby całkowite czy liczby wymierne?” uznajmy, że elementy p, r, q, s należą do liczb całkowitych. Przy oczywistym założeniu, że r i q są różne od 0. Przecież od przedszkola jest nam wpajane, że nie możemy dzielić przez 0. Relacja ~ jest wtedy opisana na iloczynie kartezjańskim dwóch iloczynów kartezjańskich zbiorów liczb całkowitych, przy czym ten wtórny jest bez 0.
~ ⊂ (ℤ× ℤ\{0})×(ℤ× ℤ\{0})
I co dalej?
Przecież już wiemy, że liczby nie kończą się na liczbach wymiernych (dodatnich lub nie). Zostały nam do scharakteryzowania jeszcze liczby algebraiczne, rzeczywiste, przestępne, zespolone. W sumie może niech liczby rzeczywiste dodatnie to będą wszelkie możliwe długości. A ujemne rzeczywiste niech będą liczbami przeciwnymi do tamtych. I jeszcze jednostka urojona, no to narysujmy sobie płaszczyznę zespoloną i mamy nawet dosyć ładnie widoczny zbiór wszystkich liczb zespolonych. Każdy punkt na ten płaszczyźnie odpowiada jakiejś liczbie zespolonej, konkretnie jednej. No i to chyba tyle. Tak? Czyli koniec eseju?
A nie chwila. Przecież są jeszcze jakieś te dziwne hebrajskie liczby. Jak on miał, alef zero? To takie śmieszne N… O, dobra mam, skopiowałem z tablicy znaków – ℵ0. Ok, ale gdzie go tu wcisnąć? Aha, to są jakieś tam liczby kardynalne. Czyli liczby, ale gdzie tu na tą płaszczyznę zespoloną je wcisnąć? No niestety nie da się. Ale przecież to nadal liczby. Mają swoje zastosowanie. Też da się je skonstruować i opisują konkretne obiekty matematyczne, zbiory. Co warto nadmienić, w tym przypadku rozpatrujemy już klasy liczb. Ma to sens, bo zaczynamy mówić o zbiorach liczb opartych na co raz to większych zbiorach. A antynomii Russella i jej konsekwencji nie trzeba nikomu przedstawiać (jest to oczywiste zagadnienie dla każdego, który spotkał się z pojęciem mocy zbioru; wytłumaczyłbym to w zadziwiający, prosty sposób, niestety, margines jest zbyt mały, by go pomieścić).
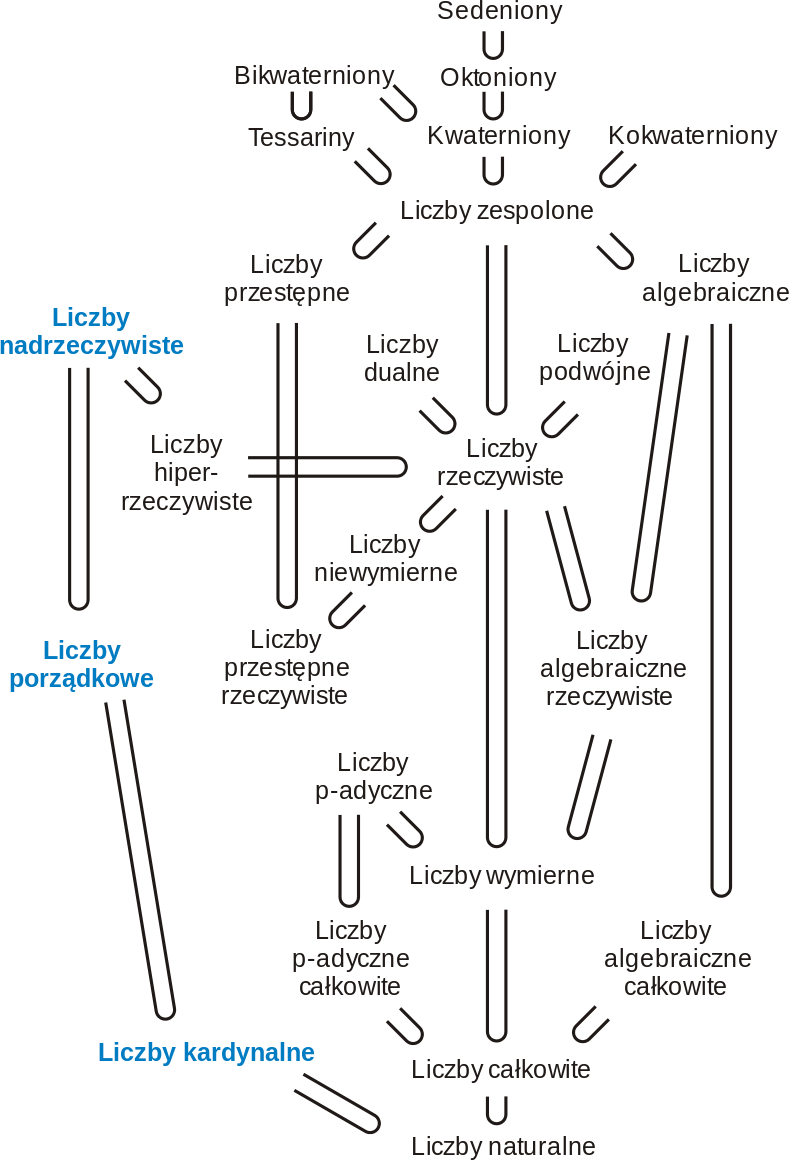
Tych liczb jak się okazuje jest trochę więcej niż się wydaje. Na Wikipedii (którą w granicach rozsądnej inspiracji się inspiruję) jest nawet bardzo ładny plik .png obrazujący te „najważniejsze” zbiory liczbowe. A raczej po prostu te najczęściej rozważane. Nad liczbami kardynalnymi są jeszcze liczby porządkowe. A kategorię wyżej ich nadklasą są jeszcze liczby hiperrzeczywiste. Ale idąc w innym kierunku, ale również od naturalnych dochodzimy do rzeczywistych, zespolonych, kwaternionów i innych liczb hiperzespolonych.
Poniżej załączam opisaną wcześniej grafikę, którą prawdopodobnie każdy znudzony student przeglądający Wikipedię wcześniej widział. A przynajmniej ci studenci, którzy wybrali ten sam temat co ja. Temat „Skąd się biorą liczby?”. Po tym długim wywodzie chyba przyszła pora. Pytanie, i odpowiedź na nie, od których zależy sens pisania tego felietonu przez ostatnie 65 minut.
Rys. 1: Diagram Hassego przedstawiający zbiory i klasy liczbowe oraz relacje zawierania między nimi.
Źródło: https://pl.wikipedia.org/wiki/Liczba
Skąd się biorą liczby?
Po dogłębnych kilku godzinach researchu i kolejnych kilku pisania dochodzimy do fundamentalnych konkluzji. Parafrazując Voltaire’a można stwierdzić, że: Gdyby nie byłoby liczby, koniecznym byłoby ją wymyśleć…
Której liczby? Tej potrzebnej akurat nam w danym momencie. Jeśli konstrukcja okaże się prawidłowa, z aksjomatów nie wyjdzie sprzeczność to nic nie stoi na przeszkodzie, by ten nowo powstały/odkryty (czy powstały czy odkryty to już temat na kolejny esej; temat, który prawdopodobnie bym wziął, gdyby trzy inne osoby mnie nie uprzedziły) zbiór lub klasę określić liczbami np. aleksowymi.
Ale co możemy powiedzieć o tych liczbach, które już „mamy”? Skąd się wzięły? Zauważmy, że wszelkie liczby w pewnym sensie pochodzą od zbioru liczb naturalnych, są jego przedłużeniem, lub wykluczeniem z jakiegoś zbioru, również skonstruowanego z liczb naturalnych. Tak jak liczby przestępne to tak naprawdę liczby rzeczywiste (skonstruowane z liczb naturalnych), które nie są liczbami algebraicznymi (które zostały również skonstruowane z liczb naturalnych).
Powiedzmy, że wszystkie inne liczby wzięły się od liczb naturalnych.
Ale wracając, skąd się wzięły liczby naturalne? Ich konstrukcja tak naprawdę zaczęła się od 0 (lub Ø). Zero, zbiór pusty, nic. Kończąc poetycko esej, wychodzi na to, że paradoksalnie… liczby wzięły się z niczego.
Dziękuję za uwagę i przeczytanie do końca krótkiej historii o historii liczb 😊